1/x est-elle discontinue en 0 ?

Télécharger la version PDF

Dans les mathématiques scolaires, la continuité d’une fonction en un point peut être appréhendée avec une certaine clarté intuitive : on pourrait, par exemple, vérifier que le graphe de la fonction, dans un petit voisinage du point examiné, n’a pas de « saut ». Cependant, des ambiguïtés se manifestent lorsqu’on se demande si certaines fonctions sont discontinues en un point donné.

Considérons le cas de la fonction $\displaystyle x\mapsto\frac1x$ définie sur $\mathbb R_0$ .

Il est bien connu que cette fonction est continue sur $\mathbb R_0$ . Mais est-elle discontinue en $x=0$ ? La réponse dépend, comme nous allons le voir, de la façon dont on a préalablement défini une fonction continue.

1. Deux définitions de la continuité et de la discontinuité

Introduisons d’emblée deux définitions possibles d’une fonction continue que l’on peut trouver, sous des formes équivalentes, dans des manuels scolaires((Pour un exemple de la définition large, voir M. Annoye, A. Van Eerdenbrugghe, CQFD Maths 5e, 6 périodes/semaine, De Boeck, 2013, p. 150. Pour la définition étroite, voir A. Adam, F. Lousberg, Espace Math 5e/6e, Théorie, Tome 1, Trigonométrie-Analyse, 6 périodes par semaine, De Boeck, 2004, p. 58.)). La raison pour laquelle nous les qualifions de « large » et d’« étroite » apparaîtra dans la suite du texte.

Définition large
Soit $f:\mathbb R\rightarrow\mathbb R$ une fonction et $a\in\mathbb R$ . La fonction $f$ est continue en $a$ si et seulement si les deux conditions suivantes sont satisfaites :

$a\in\text{dom\,} f$ ,
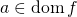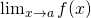$\lim_{x\rightarrow a}f(x)$ existe et vaut $f(a)$ .

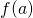Définition étroite
Soit $f:\mathbb R\rightarrow\mathbb R$ une fonction et $a\in\mathbb R$ avec $a\in\text{dom\,} f$ . La fonction $f$ est continue en $a$ si et seulement si $\lim_{x\rightarrow a}f(x)$ existe et vaut $f(a)$ .

La condition « $a\in\text{dom\,} f$ » revient à exiger que $f(a)$ existe ; elle a du sens puisque, selon la définition d’une fonction habituellement utilisée dans l’enseignement, il est possible qu’un réel n’ait aucune image par $f$ .

Pour plus de lisibilité, notons $E$ la condition « $\lim_{x\rightarrow a}f(x)$ existe et vaut $f(a)$ ». Le lecteur peut, s’il le désire, remplacer $E$ par la condition équivalente formulée en $\varepsilon$ – $\delta$ ; le contenu précis de $E$ n’aura aucune incidence sur la suite de ce texte. Réécrivons maintenant les deux définitions sous une forme qui manifeste leur structure logique.

Définition large (formulation 2)
Soit $f:\mathbb R\rightarrow\mathbb R$ une fonction et $a\in\mathbb R$ .

$\text{$f$ est continue en $a$} \quad\Leftrightarrow\quad (a\in\text{dom\,} f) \text{ et } E.$

Définition étroite (formulation 2)
Soit $f:\mathbb R\rightarrow\mathbb R$ une fonction et $a\in\mathbb R$ avec $a\in\text{dom\,} f$ .

$\text{$f$ est continue en $a$} \quad\Leftrightarrow\quad E.$

Nous voyons que la seule différence entre ces énoncés est que dans le premier, la condition « $a\in\text{dom\,}f$ » vient après le « $\textcolor{white}{|}\!\!\!\Leftrightarrow$ ».

Nous allons maintenant considérer que la discontinuité est la négation logique de la continuité, c’est-à-dire que « $f$ est discontinue en $a$ » est vrai si et seulement si « $f$ est continue en $a$ » est faux. Il découle alors de ce qui précède les deux définitions suivantes de la discontinuité en un point :

Définition large (formulation 3)
Soit $f:\mathbb R\rightarrow\mathbb R$ une fonction et $a\in\mathbb R$ .

$\text{$f$ est discontinue en $a$} \quad\Leftrightarrow\quad (a\notin\text{dom\,} f) \text{ ou } (\text{non\,} E).$

Définition étroite (formulation 3)
Soit $f:\mathbb R\rightarrow\mathbb R$ une fonction et $a\in\mathbb R$ avec $a\in\text{dom\,} f$ .

$\text{$f$ est discontinue en $a$} \quad\Leftrightarrow\quad \text{non\,} E.$

Sur base de la définition large, une fonction est toujours discontinue en tout point hors de son domaine de définition. Par contre, selon la définition étroite, la notion même de discontinuité en $a$ présuppose que $a$ fasse partie de $\text{dom}\, f$ de sorte qu’il n’y a pas de sens à parler de discontinuité en dehors de $\text{dom}\, f$ . Dans le cas de la fonction $1/x$ , nous avons donc que :

selon la définition large, 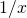$1/x$ est discontinue en $x=0$ ,
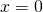selon la définition étroite, on ne peut rien dire sur la continuité, ni la discontinuité, de 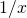$1/x$ en $x=0$ .

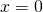Ce que l’on dit de $1/x$ en $x=0$ dépend donc de la définition adoptée. Cette absence de consensus est plutôt surprenante quand on considère que cette fonction fait partie du b.a.-ba du mathématicien.

2. Les différentes saveurs de l’idée de discontinuité

Tant que l’on examine la (dis)continuité en un point $a$ du domaine de la fonction, les différentes définitions précédentes fournissent les mêmes conclusions : une fonction est continue en $a$ au sens large si et seulement si elle l’est au sens étroit (et de même pour la discontinuité en $a$ ). Par contre, les définitions diffèrent sur le caractère discontinu si $a$ est hors du domaine.

En réalité, la discontinuité au sens large permet de saisir deux idées intuitives d’une courbe qui « saute » :

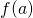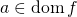le fait qu’il y ait un « saut » entre $f(a)$ et au moins une limite latérale en $a$ (si $a\in\text{dom\,} f$ ), comme ici :
Figure A
le fait que $\text{dom\,} f$ soit topologiquement non connexe, comme ici :
Figure B

Au fond, il s’agit de deux phénomènes différents. En effet, le premier concerne le comportement d’une fonction sur son domaine tandis que le second ne concerne que la forme (topologique) du domaine, indépendamment du comportement de la fonction $f$ définie dessus.

La définition large permet de dire, dans les deux cas, que $f$ est discontinue en $a$ . La définition étroite, elle, ne le permet que dans le cas A (d’où les qualificatifs « large » et « étroit »). Examinons maintenant ce que cela implique pour chaque définition.

2.1. Ce qu’implique la définition large

Cette définition permet de consolider l’idée selon laquelle une courbe discontinue en $a$ est une courbe « que l’on ne peut pas dessiner d’un seul trait autour de $a$ ». Par exemple, dans les figures A et B ci-dessus où l’on ne peut effectivement pas tracer toute la courbe sans lever le crayon, cette définition permet de déclarer que $f$ est discontinue en $a$ .

Cependant, elle a des conséquences dans d’autres situations probablement inattendues, comme par exemple celle où $\text{dom}\, f$ est connexe, mais où $a\notin\text{dom}\, f$ :

Ici, la définition large nous oblige à dire que $f$ est discontinue en $a$ , ce qui peut sembler étrange (par exemple, $\sqrt x$ serait discontinue en $-10$ ). Le cas de la fonction vide, où $\text{dom\,} f=\emptyset$ , est loufoque : elle est discontinue partout ! Pour distinguer les situations intéressantes des situations triviales, il serait alors nécessaire d’introduire différents types de points de discontinuité. On pourrait par exemple considérer spécifiquement les points $a\notin\text{dom\,}f$ tels que $]a-\varepsilon,a[$ et $]a,a+\varepsilon[$ sont inclus dans $\text{dom\,}f$ ; c’est le cas de $0$ pour la fonction $x\mapsto\frac1x$ .

Remarquons aussi que la définition large peut provoquer une confusion linguistique. En effet, dans le milieu mathématique, l’usage veut que « fonction continue » soit synonyme de « fonction continue sur son domaine de définition ». La fonction $1/x$ fait donc bien partie de la classe des fonctions continues. Mais s’il est légitime, conformément à la définition large, d’évaluer sa (dis)continuité en $x=0$ , il pourrait alors sembler déroutant, pour un élève, d’admettre qu’elle soit en même temps « continue » et « discontinue en $0$ ». Ce problème ne se présente pas avec la définition étroite.

2.2. Ce qu’implique la définition étroite

Selon cette définition, le simple fait qu’une courbe ne puisse pas être tracée « d’un seul trait » ne suffit pas pour pouvoir déclarer qu’elle est discontinue en un point. Par exemple, dans la figure B, cette définition ne permet pas de déclarer que $f$ est discontinue en $a$ .

La définition étroite est, en un certain sens, plus rigoureuse dans la terminologie qu’elle pose. En effet, on peut penser que la non-connexité d’un domaine est une propriété du domaine lui-même et non d’une fonction définie dessus. Par conséquent, dire qu’une fonction $f$ est discontinue simplement parce que son domaine est non-connexe serait attribuer à $f$ une propriété qui, en réalité, ne relève pas de cette fonction : en effet, tout autre fonction sur le même domaine (non-connexe) devrait également être déclarée discontinue. La définition étroite va dans le sens de cette observation en restreignant la notion de discontinuité de façon à en faire une authentique propriété de la fonction examinée et de son comportement.

Enfin, si l’on tient compte de la définition topologique, plus générale, de la continuité, alors la définition étroite sera préférable. En effet, dans le contexte topologique, les fonctions sont toutes des applications, c’est-à-dire des fonctions où tout élément du domaine possède exactement une image. La continuité n’y est donc définie qu’en des points $a$ où $f(a)$ existe et seule la définition étroite est compatible avec cette approche.

3. Conclusion

Lors de l’apprentissage d’un concept nouveau, s’il est important d’en voir des exemples, il est tout aussi essentiel d’étudier des contre-exemples. Dans le cas du concept de continuité, comme nous l’avons vu, les contre-exemples admissibles dépendent des définitions choisies, ce qui peut engendrer des confusions chez un élève lorsque, au fil des années, ses professeurs adoptent des définitions différentes. Si une difficulté de ce type se présentait, revenir explicitement sur la définition de la continuité pourrait aider à lever des malentendus.

Dans tous les cas, quelles que soient les définitions adoptées, distinguer les situations de non-connexité des autres cas de discontinuité devrait déjà éclaircir les idées.

1/x est-elle discontinue en 0 ?

1. Deux définitions de la continuité et de la discontinuité

2. Les différentes saveurs de l’idée de discontinuité

2.1. Ce qu’implique la définition large

2.2. Ce qu’implique la définition étroite

3. Conclusion

Laisser un commentaire Annuler la réponse.

Matière

Niveau

Type d'article