Abus de langage usuels dans le discours sur les vecteurs

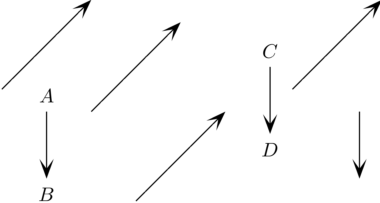
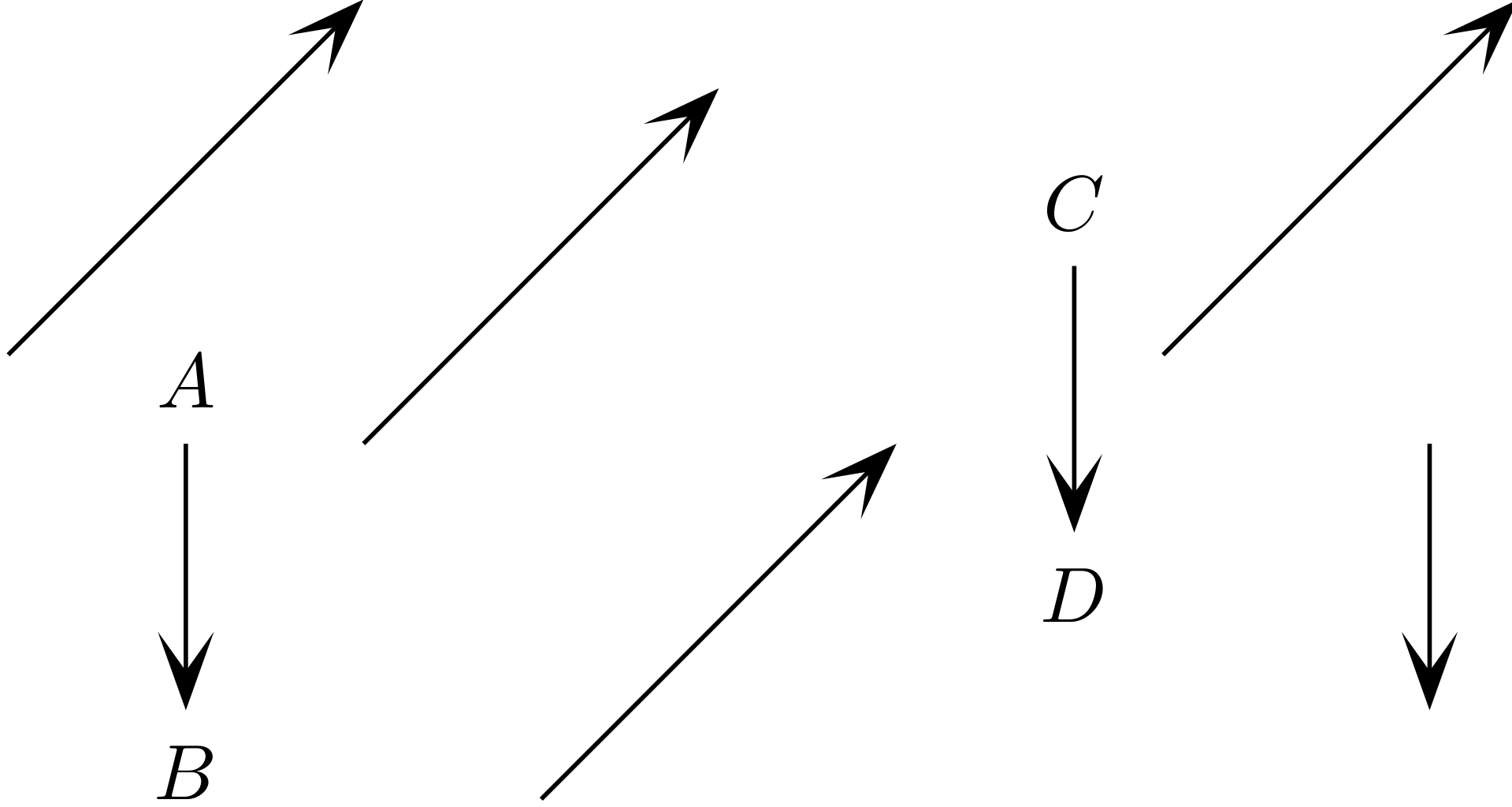
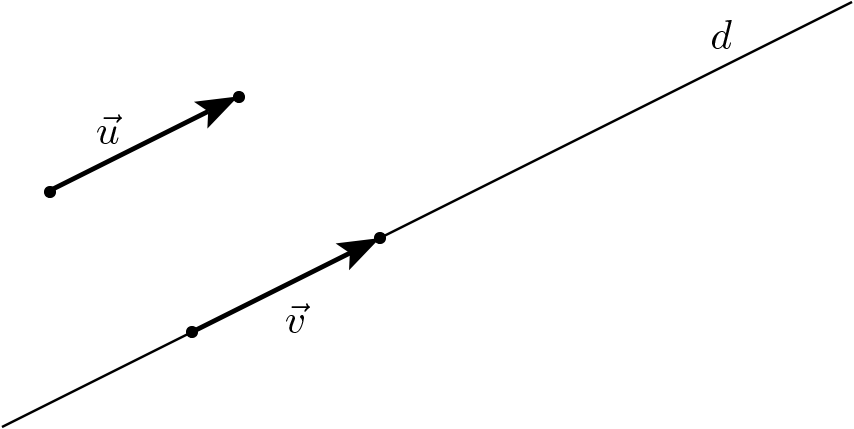
Sur le schéma suivant, on peut distinguer sept segments orientés, mais seulement deux vecteurs :

En particulier, les segments orientés allant de à et de à sont différents, puisqu’ils occupent des positions différentes dans le plan, mais ils représentent ((Dans ce texte, nous mettrons les formes du verbe « représenter » en italique lorsqu’il doit être compris au sens mathématique d’un segment orienté qui représente un vecteur, ce dernier étant défini comme un ensemble de segments orientés ayant la même direction, le même sens et la même longueur.)) géométriquement le même vecteur, ce qu’exprime l’égalité . Il y a donc une différence conceptuelle entre un segment orienté et un vecteur, et comprendre cette différence peut constituer une tâche difficile pour un élève qui découvre cette matière. (Voir l’article La notion de vecteur et la signification du verbe « représenter ».)

Cependant, notre façon courante de parler des vecteurs tend à entretenir leur identification avec les segments orientés, par l’usage répété de certains abus de langage qui donnent l’impression qu’un vecteur occupe bel et bien une position précise dans le plan. Voici quelques-uns de ces abus.

1. « L’origine et l’extrémité d’un vecteur »

Lorsqu’on est en présence d’un vecteur , il est courant de dire que les points et sont respectivement « l’origine » et « l’extrémité » de ce vecteur. Comme ces points possèdent une position précise dans le plan, cet usage peut donc donner l’impression — mathématiquement erronée — qu’un vecteur est lui-même positionné dans le plan, puisqu’il « relie » ces deux points. Des schémas tels que le suivant sont monnaie courante et consolident cette impression

Mais remarquons que sur ce schéma, nous pourrions tout aussi bien mettre l’étiquette «  » à la place de «  » (puisque nous avons l’égalité stricte ). Le résultat semblerait cependant incongru puisqu’il choquerait le sentiment intuitif (mais erroné) qu’un vecteur est rattaché à « son origine » et à « son extrémité ».

En effet, un vecteur ne peut être attaché à un point du plan et de ce fait il ne peut avoir ni point d’origine ni point d’extrémité qui le cloisonneraient. Seul un représentant de ce vecteur peut donc avoir une origine et une extrémité. Bien que toujours erronée, il serait préférable de nommer un vecteur à l’aide d’une lettre minuscule comme par exemple . Cette notation aurait, malgré ses défauts, l’avantage de ne pas inciter les élèves à associer des points du plan précis à un vecteur.

En réalité, bien sûr, l’expression « l’origine du vecteur  » est un abus de langage. Rigoureusement parlant, elle est un raccourci pour parler de « l’origine du segment orienté qui relie à et qui représente le vecteur  ». Mais il est important d’avoir conscience de ce raccourci, sans quoi l’on risque de se perdre dans un langage vide de sens.

2. Des vecteurs « consécutifs » ou « de même origine », la relation de Chasles

Dans l’énoncé de la relation de Chasles qui définit la somme de deux vecteurs, il est courant de parler de vecteurs « consécutifs », c’est-à-dire dont « l’origine du second coïncide avec l’extrémité du premier », ou encore de vecteurs « de même origine ». Ces expressions constituent de nouveau des abus de langage qui reposent sur, et consolident en même temps, l’abus déjà décelé dans la section précédente. Si elles étaient prises à la lettre, elles seraient de nouveau vides de sens.

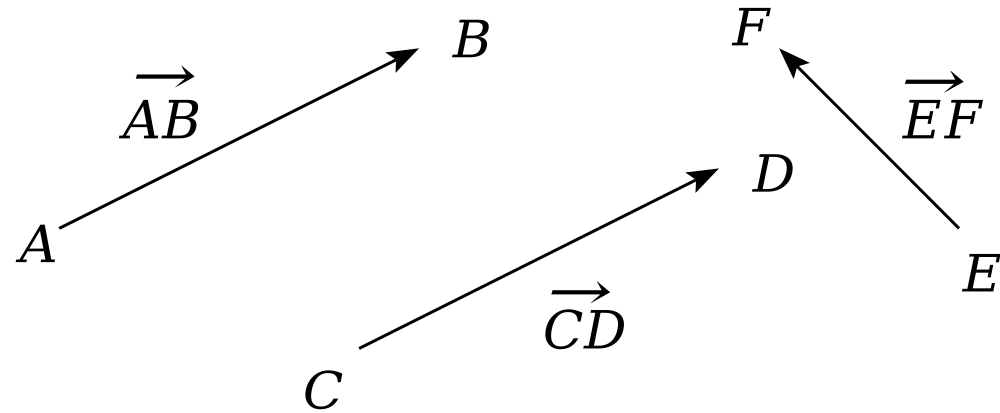
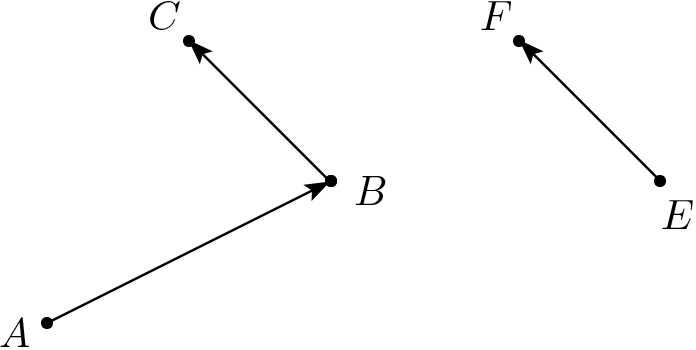
Par exemple, nous pourrions parfaitement déclarer que deux vecteurs quelconques sont toujours consécutifs (ou de même origine). En effet, sur base du schéma suivant :

nous pourrions affirmer que les vecteurs et sont consécutifs : en effet, et sont consécutifs, or est identique à , donc s’ensuit la conclusion. Mais nous voyons qu’à nouveau, nous sommes tombés dans la trivialité, ce qui montre que l’idée même de « vecteurs consécutifs » n’a aucun contenu.

Sémantiquement parlant, seuls deux segments orientés peuvent être consécutifs (ou de même origine), et jamais deux vecteurs. L’abus de langage dont il est ici question incite donc fortement à prendre les vecteurs pour de simples segments orientés, avec toutes les confusions que cela peut susciter. En particulier, et ceci est un problème couramment observé, un élève risquerait d’être incapable d’effectuer une somme de deux vecteurs représentés par deux segments orientés non consécutifs. Dans le meilleur des cas, il retiendrait qu’il a le « droit » de déplacer (par translation) les vecteurs pour les « attacher », mais il ne s’agirait-là que d’une règle pratique sans grande signification mathématique.

3. Des droites qui « contiennent » des vecteurs

Un autre abus de langage consiste à déclarer qu’un vecteur est contenu dans une droite. Par exemple, cette idée peut servir à parler de vecteurs « parallèles » ou de vecteurs orthogonaux, comme l’illustre l’extrait suivant d’un manuel :

Deux vecteurs non nuls sont parallèles ssi les droites qui les contiennent sont parallèles.
Deux vecteurs non nuls sont orthogonaux ssi les droites qui les contiennent sont perpendiculaires.
(J.-M. Danel, V. Demezel, Astro-math 4, Waterloo : Plantyn, 2011, p.~49.)

Mais encore une fois, cet usage engendre potentiellement des trivialités. En effet, nous pourrions parfaitement affirmer que la droite ci-dessous contient le vecteur , puisqu’elle contient et que est identique à  :

Faut-il encore parler de droites qui « contiennent » des vecteurs dans de telles circonstances ?

De nouveau, à strictement parler, une droite ne peut contenir un vecteur puisque ce dernier n’est pas situé dans le plan ; elle peut au mieux contenir un segment orienté qui représente ce vecteur. La notion de parallélisme ne s’applique qu’aux segments orientés (pour les vecteurs, on parlera plutôt de colinéarité). Parler de « la droite qui contient un vecteur » est donc un abus de langage et s’il n’est pas saisi comme tel, il risque d’alimenter la confusion entre les vecteurs et les segments orientés.

4. L’abus final : les noms de vecteurs dans les schémas graphiques

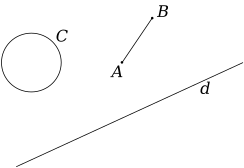
Lorsque nous représentons graphiquement un objet, il est d’usage d’écrire son nom à côté de sa représentation graphique, comme on le voit sur ce schéma représentant un cercle, un segment et une droite :

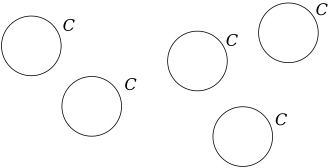
A priori, deux objets isométriques mais occupant deux positions différentes sont considérés comme des objets différents et doivent, par conséquent, recevoir des noms différents. Les notations sur le schéma suivant sont donc, en principe, mal choisies car on ne sait plus quel cercle est désigné par la lettre «  » :

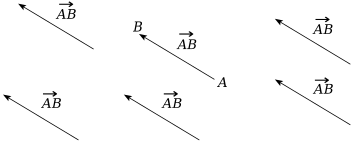
Pourtant, on pourrait se permettre de le faire avec les noms de vecteurs : en effet, sur le schéma suivant, toutes les flèches représentent le même vecteur  :

Ceci montre à quel point le statut du nom d’un vecteur diffère de celui de tous les autres noms de figures géométriques classiques. L’écart provient du fait que si une flèche, en tant que signe graphique, dénote un segment orienté, le nom «  » ne désigne pas ce segment orienté ; ils ne peuvent donc pas figurer côte à côte sur un schéma.

À strictement parler, un vecteur ne peut jamais être graphiquement tracé puisqu’il n’occupe aucune position précise dans le plan. Par conséquent, si l’on veut maintenir des usages cohérents en matière de notation, il ne faudrait donc jamais écrire un nom de vecteur comme «  » ou «  » dans un schéma.