L’étude des nombres premiers pour un jeune élève peut être frustrante et contre-intuitive. Frustrante d’abord, parce que certaines des définitions que l’on en donne sont suffisamment ambigües que pour placer un élève au raisonnement correct en porte-à-faux avec l’enseignant. Contre-intuitive ensuite, vu l’indéniable association qu’il existe dans le langage courant entre le nombre 1 et « premier ».
Avançons au départ d’une définition, afin d’ôter toute confusion et de comprendre pourquoi, dans certains cas, l’élève qui pense 1 premier a toutes les raisons de le croire. Précisons d’emblée que les nombres dont il est question ici sont les nombres naturels.
Soit la définition suivante, libre interprétation de ce qu’on entend communément à propos des nombres premiers :
Définition 1
Un nombre premier est un nombre qui n’est divisible que par lui-même, et par 1.
En première approximation, on pourrait certainement considérer cette définition comme correcte. L’une des causes est qu’on peut la voir comme une version modernisée de la définition d’Euclide (la modernité ayant apporté le vocabulaire contemporain, et la divisibilité par 1) 1.
La première définition entraîne logiquement que 1 est un nombre premier. Le nombre 1 vérifie en effet les deux conditions qu’elle décrit :
- 1 est divisible par lui-même ;
- 1 est divisible par 1.
Comment en vouloir aux élèves qui envisagent les choses de cette façon ?
Au quotidien, lorsqu’on parle de deux objets dans la même phrase, ces objets existent et sont différents. Interprétée dans le langage courant, la définition 1 peut donc être considérée comme correcte. Mais au cours de mathématiques, on ne peut raisonnablement pas demander aux élèves de remplacer une bonne intuition logique par un implicite du langage courant !
Le problème ne vient donc pas de la compréhension des apprenants, mais bien de la définition en elle-même, qui du point de vue logique ne spécifie absolument pas que les deux diviseurs évoqués doivent être différents.
1. Le statut particulier de « un »
Les nombres premiers sont ceux à partir desquels on produit tous les autres par multiplication.
Conventionnellement, 1 est écarté de cette liste afin de rendre unique la décomposition de tout nombre en un produit de facteurs premiers.
Exemple :
- Avec 1 non-premier, 6 se décompose de façon univoque en
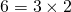 .
. - Avec 1 premier, 6 se décomposerait en
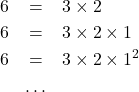
Considérer 1 comme premier aurait pour inconvénient de réduire le domaine d’application d’une majorité des définitions, propriétés et théorèmes d’arithmétique aux nombres premiers supérieurs ou égaux à 2… et il conviendrait d’apporter cette précision à chaque fois 2.
La convention qui consiste à exclure 1 trouve ses racines chez Euclide, qui distinguait 1 (l’unité) des nombres (les « multitudes », regroupements d’unités) 1. Les définitions arithmétiques euclidiennes ne laissaient donc aucune confusion possible, puisque 1 ne faisait pas partie du domaine d’application qu’elles recouvraient. En particulier, la première définition donnée dans ce document ne laisse place à aucune confusion si le nombre 1 n’est pas à prendre en considération.
Remarque
Les nombres non premiers sont parfois dits « composés », mais attention : ceci ne fait pas de 1 un nombre composé pour autant. Un nombre composé doit pouvoir s’écrire comme un produit de facteurs premiers 3. Ce n’est pas le cas de l’unité (même si on la considère aujourd’hui comme un nombre). Une fois encore, 1 bénéficie d’un statut particulier.
2. Deux, au moins deux
Faisons apparaître de façon claire la nécessité d’avoir deux diviseurs distincts :
Définition 2
Un nombre premier est un nombre qui a deux diviseurs : 1 et lui-même.
Et soyons même scrupuleux !
Définition 3
Un nombre premier est un nombre qui possède deux diviseurs distincts : 1 et lui-même.
Sommes-nous désormais tirés d’affaire ? Pas si sûr.
Questions :
- 6 possède-t-il deux diviseurs ? Oui, par exemple 2 et 6
- 6 possède-t-il deux diviseurs distincts ? Oui, 2 et 6 sont distincts
- 6 possède-t-il deux diviseurs distincts, dont 1 et lui-même ? Oui, 1 et 6 sont des diviseurs distincts de 6
D’après notre dernière définition, 6 est donc un nombre premier !
Remarquons que pour en arriver à cette conclusion, il a été nécessaire de traduire les « deux points » de la définition par un mot indiquant une inclusion (ici : « dont »). Traduction certes artificielle, mais pas incorrecte.
Le problème ne vient pas de cette traduction, mais de la façon de comprendre le « deux », à mettre en lien avec la compréhension du « un » en mathématiques. Dans le langage courant, lorsqu’on précise que deux objets satisfont une propriété, on sous-entend qu’il n’en existe pas d’autres (à moins qu’on l’explicite formellement).
Pourtant, mathématiquement parlant, la propriété « avoir deux diviseurs (distincts) » est vraie dès que le seuil de deux diviseurs est atteint. Il faut comprendre « deux » comme « au moins deux ». Ce qui conduit à considérer 6 comme un nombre premier. Dans la définition de nombre premier, le « deux » risque d’être compris de cette manière également, à tort. Mieux vaut spécifier dès le départ qu’être premier requiert de posséder deux diviseurs, ni plus ni moins. Remplaçons donc notre « deux » diviseurs distincts » par « exactement deux diviseurs ».
3. Vers une définition finale
Définition 4
Un nombre premier est un nombre qui possède exactement deux diviseurs : 1 et lui-même.
Toute ambiguïté est désormais levée.
On remarquera néanmoins que le « 1 et lui-même » n’est pas absolument nécessaire, puisque tout nombre (premier ou non) est divisible par 1 et par lui-même.
On peut donc se contenter de cette dernière définition, présente dans la littérature 4 :
Définition 5
Un nombre premier est un nombre qui possède exactement deux diviseurs.
Nous admettrons cependant que la définition 5 est sans doute peu adaptée à des élèves apprenant ce que sont les nombres premiers, bien qu’elle soit correcte et succincte. Ne nous privons dès lors pas de conserver le « 1 et lui-même » à des fins d’illustration et de clarté.

