Y a-t-il plus d’un moins ?

Au fil de son parcours scolaire, l’élève rencontre différents usages du symbole « – ». Il suffit pour s’en convaincre de constater que ce symbole recouvre des significations sensiblement différentes dans des expressions comme « 5−2 », « −2+5 » et « −a ». L’élève qui n’est pas conscient de ces différentes significations peut par exemple rencontrer des difficultés à concevoir que « −a » ne désigne pas nécessairement un nombre négatif.

Cet article vise à dégager certaines des significations que peut recouvrir le symbole « − », à montrer que cette polysémie peut être la source de difficultés didactiques et à proposer quelques pistes permettant d’y remédier.

1. Polysémie du symbole « − »

Les recherches menées en didactique des mathématiques tendent à distinguer trois significations du symbole moins : le moins de soustraction, le moins de symétrie et le moins indiquant le caractère négatif d’un nombre ^1,2.

Définition 1 : Moins de soustraction
Le symbole « − » désigne l’opération qui à un couple de nombres associe leur différence. Ce symbole de fonction binaire (qui admet deux arguments) est noté de façon infixe (c’est-à-dire qu’il se place entre les arguments). Ainsi, si «  » et «  » sont des expressions qui désignent des nombres, l’expression «  » désigne le résultat de la soustraction du second nombre au premier.

Définition 2 : Moins de symétrie
Le symbole « − » désigne l’opération qui à un nombre associe son opposé. Ce symbole de fonction unaire (qui admet un unique argument) est noté de façon préfixe (c’est-à-dire qu’il se place devant l’argument). Ainsi, si «  » est une expression qui désigne un nombre, l’expression «  » désigne l’opposé de ce nombre.

Définition 3 : Entier négatif
Le symbole « − » préfixé à une expression numérique ((Une expression numérique est ici définie comme une suite finie non vide de chiffres, ne commençant pas par «  » si elle contient plusieurs chiffres. En ce sens, les expressions «  » , «  » et «  » ne sont pas des expressions numériques.)) désigne un nombre entier négatif. La combinaison de ce symbole et d’une expression numérique forme un unique symbole de constante. Ainsi, si «  » est une expression numérique qui désigne le -ième nombre entier supérieur à zéro, l’expression «  » désigne le -ième nombre entier inférieur à zéro.

Remarque
Lorsqu’il indique le caractère négatif d’un nombre entier, le symbole « − » possède un statut structurel ³. Autrement dit, il ne peut être dissocié de l’expression qu’il précède et dont il fait partie intégrante. Aussi, il ne doit pas être confondu avec un symbole d’opération ^4,5.

Afin d’illustrer ces différentes interprétations du symbole moins, analysons l’expression ci-dessous.

«  »

Cette expression peut être interprétée comme l’opposé de la différence du nombre entier négatif (désigné par) «  » et du nombre (désigné par) «  ». Selon cette interprétation, chacune des apparitions du symbole « – » dans l’expression qui précède possède une signification différente des deux autres.

• La première occurrence est un symbole de fonction unaire qui désigne l’opération consistant à associer à un nombre son opposé (cf. Définition 2).
• La seconde occurrence suivie du symbole « 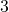 » forme un unique symbole de constante qui désigne le troisième nombre entier inférieur à zéro (cf. Définition 3).
• La troisième occurrence est un symbole de fonction binaire qui désigne l’opération consistant à associer à un couple de nombres leur différence (cf. Définition 1).

2. Difficultés didactiques

Les difficultés liées à l’apprentissage des différents usages du symbole « − » sont nombreuses et enchevêtrées. L’objet de cette section est d’en proposer une classification à partir de certaines études réalisées en didactique des mathématiques ^1,6. Nous distinguons trois catégories de difficultés conceptuellement hiérarchisées (cf. Figure 1 ).

2.1. La notation et la portée d’une occurrence du symbole « − »

La première catégorie de difficultés concerne l’identification de la structure d’une expression algébrique. Ces difficultés ont trait exclusivement à la syntaxe de la langue mathématique et sont antérieures à l’interprétation sémantique des symboles qui la composent. En principe, la structure syntaxique d’une expression algébrique peut être déterminée de façon univoque au moyen des parenthèses et des règles d’écriture gouvernant les symboles d’opération.

De ce point de vue, il existe seulement deux notations du symbole « − » ; l’une est infixe (cf. Définition 1) et l’autre est préfixe (cf. Définitions 2 et 3). En plus d’identifier les occurrences infixes et préfixes du symbole « − », l’élève doit être capable d’identifier les expressions sur lesquelles portent ces occurrences.

Exemple (La notation infixe du symbole « − »)
Dans l’expression «  », quelles sont les expressions sur lesquelles porte l’occurrence du symbole « − » ? Deux découpages syntaxiques sont a priori envisageables. L’un, qui est conforme aux règles d’écriture, revient à assimiler l’expression considérée à «  » et l’autre, qui les transgresse, revient à assimiler cette expression à «  ». Dans le premier cas, l’occurrence du symbole moins porte sur «  » et «  » alors que, dans le second cas, elle porte sur «  » et «  ».

Exemple (La notation préfixe du symbole « − »)
Quelle est l’expression sur laquelle porte l’occurrence du symbole « − » figurant dans «  » ? Sans tenir compte des règles d’écriture, deux structures syntaxiques peuvent être associées à cette expression. L’une, qui est correcte, est semblable à celle de l’expression «  ». L’autre, qui est erronée, est semblable à celle de «  ». Dans le premier cas, l’occurrence du symbole moins porte sur «  » alors que, dans le second cas, elle porte sur «  ».

2.2. L’interprétation d’une occurrence du symbole « − »

La structure d’une expression algébrique une fois identifiée, une seconde source de difficultés concerne l’interprétation sémantique qu’il convient d’attribuer aux apparitions du symbole « − ». Dans la mesure où seul le moins de soustraction est noté de façon infixe, la signification d’une occurrence utilisée de la sorte ne pose pas de véritable problème. Pour ce qui est d’une occurrence utilisée de façon préfixe, la situation est plus délicate puisque deux significations distinctes peuvent lui être attribuées : le moins de symétrie et le moins indiquant le caractère négatif d’un nombre. Nous centrerons donc notre propos sur ce dernier cas de figure.

Lorsque les nombres entiers sont introduits en première secondaire, les élèves sont confrontés pour la première fois à une signification du symbole moins autre que celle de la soustraction. En dehors de cette opération, ce symbole est alors utilisé indifféremment pour désigner l’opposé d’un nombre naturel ou indiquer son caractère négatif. Il faut bien souvent attendre l’apparition d’expressions plus complexes (où le symbole moins précède par exemple une expression entre parenthèses ou une expression littérale) pour que le moins utilisée de façon préfixe soit employé dans un contexte plus large, où les deux significations qu’il peut recouvrir ne sont plus systématiquement interchangeables.

L’apparition tardive d’expressions plus élaborées peut induire chez l’élève une représentation mentale erronée où le concept de nombre opposé est assimilé à celui de nombre négatif ⁷. Autrement dit, la signification du moins de symétrie et du moins indiquant le caractère négatif d’un nombre entier sont pour lui interchangeables. L’élève devra donc apprendre à discriminer les contextes où ces deux significations sont équivalentes et ceux où elles ne le sont pas. À cet égard, remarquons que toute occurrence du symbole moins indiquant le caractère négatif d’un nombre peut également être interprétée comme un moins de symétrie alors que la réciproque n’est pas vraie.

Exemple (Le symbole « − » suivi d’une expression littérale ou d’une expression entre parenthèses)
Nombreux sont les élèves qui rencontrent des difficultés à concevoir que «  » désigne un nombre positif et que l’expression «  » est vraie pour certaines valeurs de dans les entiers.

2.3. Les relations entre les significations du symbole « − »

Dégager la structure syntaxique d’une expression algébrique et assigner une signification adéquate aux occurrences du symbole « − » qui y figurent ne suffisent pas à transformer une expression en une autre qui lui est égale. Pour cela, il est en outre nécessaire de maîtriser les relations que ces significations entretiennent entre elles et avec les autres opérations.

À titre d’exemple, examinons une résolution d’équation où les trois significations du symbole moins apparaissent ² :

Nous constatons alors que les occurrences du symbole moins figurant dans ces équivalences logiques sont successivement un moins de soustraction, un moins de symétrie et un moins pouvant être conçu à la fois comme un moins de symétrie et comme indiquant le caractère négatif d’un nombre.

Montrer que si et seulement si permet d’expliciter les relations entre le moins de soustraction et le moins de symétrie. Il est possible de déduire cette équivalence en utilisant entre autres le fait que, pour tout et pour tout , et .

D’autre part, montrer que si et seulement si permet d’expliciter les relations entre le moins de symétrie et le moins indiquant le caractère négatif d’un nombre. Il est possible de déduire cette équivalence à partir du fait que, pour tout , .

Dans le but de permettre à l’enseignant qui le souhaiterait, nous proposons des idées d’exercices de diagnostic et des pistes didactiques dans un article dédié.